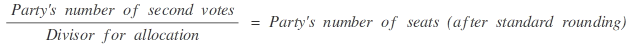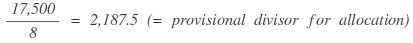(1) 앞으로 12년~16년은 지속적으로 선거 제도 (국회의원, 대통령제)를 개혁해야 한다. 일회적으로 끝내서는 안된다.
선거개혁은 2020년, 2024년, 2028년 계속되어야 한다. 민주당 사이비 학자들과 이데올로그들이 퍼뜨리는 망상처럼, 대통령 제도와 독일식 '혼합 비례대표제도'가 상충되는 것은 아니다. 각 국가의 선거제도는 그 나라 사람들의 '민주주의 실천 의지'와 '실력'에 따라 창조적으로 형성된다.
(2) 민주당 일부 사이비 선거공학자들의 머리 속에는 '사회 혼란 가중' 대통령 흔들기라는 과장만이 들어있다.
그런 억지 비과학적 주장은 뒤로 하고, 김대중, 노무현 전 대통령이 선호했던 '독일식 권역별 비례대표제도, 즉 지역 후보와 비례대표제도를 혼합한 (MMP mixed member proportional )선거제도의 특징을 간략히 살펴보자. 현재 한국에서 논의되는 ‘연동형 비례대표제도’는 독일식 권역별 비례대표제와 유사하기 때문이다.
(3) 왜 독일식이 중요한가?
독일식 '혼합형 비례대표제도'는 새로운 창조적 '잡종' 형태이고, 김대중-노무현 대통령이 언급한 것처럼 언젠가 한번쯤은 반드시 거쳐가야 하는 통로이다.
한국은 아직 순수 비례대표제도 (네덜란드 등)를 채택하기는 힘들다. 유권자들이 지역 후보를 뽑고 싶어 하기 때문이다. 한국에게 어느 한 나라 선거모델이 정답이겠는가? 독일식을 참고해서 새로운 한국 선거제도를 만들어야 한다.
독일 선거 특징은 당선 의원 숫자가 선거마다 변화된다는 데 있다. 지역구 후보 당선자는 299명으로 정해져 있지만, 비례대표는 299명을 넘는다. 그 이유는 독일 선거 방식이 순수비례도 아니고, 가장 비민주적인 '승자독식' 제도도 아니기 때문이다.
2017년 9월 총선 결과 총 의원 숫자는 독일 유권자 인구 7338만명에 709명이었다. 지역 299명, 비례대표 299명에서 출발했는데, 왜 111명이나 더 늘어났는가? 독일 선관위는 왜 의원 숫자를 줄이지 않고, 늘리는 방식으로 투표 등가성을 높이려고 했는가?
- 독일은 지역구 후보는 16개 각 주별에 퍼진 299개 선거구에서 선출된다.
- 그런데 비례대표 당선자는 299명을 넘는다. 그 이유는 두 가지 이유에서 비롯된다. 하나는 초과 의석 때문에 늘어난 숫자이고, 두번째는 각 권역별이 아니라, 전국적으로 정당투표 비율을 계산해서, 각 정당에 '보정 (보상)'해주기 때문이다.
이 보정 의석 역시 정당 명부 비례대표이다. 초과 의석 때문에 발생한 정당 간 불비례성을 '보상'하기 위해서 마지막 절차로 '전국 정당 투표율'에 따라 각 정당에 의석을 추가해준다.
- 처음 출발: 16개 주 권역별 배당 의석수는 각 주의 '인구 총수'에 따라 결정되었다. 배정: 299석, 비례 299석, 총 598석으로 시작했다.
- 최종 결과 709 석은 어떻게 구성되었는가?
(1) 299석: 최종 의석수는 지역구 당선 숫자는 변화가 없다. 299석이다.지역 후보자 당선 299명 중, 기민당(CDU) 185명 , 기사련( CSU) 46명 , 사민당(SPD) 59명, 좌파당 (die Linke) 5명, 녹색당 (Grüne) 1명, 독일을 위한 대안(AfD) 3명, 자유민주당 (FDP) 0 석을 획득했다.
(2) 46석 (비례명부에서) : 그런데 각 16개 주 (권역별)에서 초과 의석 숫자가 발생할 경우는, 전체적으로 비례대표가 늘어난다.
초과 의석이 발생하는 이유는 각 권역에서 한 정당이 획득할 수 있는 최대 의석 숫자를 결정하는 기준 때문이다. 정당 투표율에 따라 정당이 획득가능한 당선자 숫자가 정해진다.
예를들어, 만약 정당 A가 정당투표율에 따라 최대 6석을 가져가야 하는데, 지역 당선자를 8명을 배출했을 경우가 발생하면, 그 정당은 그 권역에서 6명이 아니라 8명 당선자를 내게 된다.
(8 빼기 6 = 2명의 초과 의석이 생긴다)이렇게 16개 주에서 생겨난 초과의석 수가 46석이었다. 이 46석 역시 각 정당별 비례대표 명단에 따라 배정된다.
(3) 644석: 그렇다면 지금까지 확정된 각 정당별 '최소 보장 의석'수를 다 합치면, 지역구 299명 + 초과 비례 46석 + 원래 배정된 299 비례대표 의석 644석이다.소결: 644석에는 지역구 299석과 비례 345석이 포함된다.
(4) 보상 (보정: Ausgleichung) 의석 제도를 2013년 2월 21일 개정된 독일연방선거법에 따라 도입했다.
그 이유는 초과의석이 선거마다 지속적으로 증가함에 따라, 초과의석을 가진 정당이 그렇지 않은 정당에 비해 과도하게 대표되는 '약점'이 드러났기 때문이다.
2017년 총선에서 초과 의석을 발생시킨 정당은 기민당 (CDU) 36석, 기사련 (CSU) 7석, 사민당 (SPD) 3석이었다.
이러한 불비례성을 막기 위해서, 16개 권역이 아닌 독일 전국 정당투표 숫자와 644석과의 비율을 따져서, 각 정당에 돌아갈 '보상 의석' 숫자를 결정한다.
CDU 가 이미 위에서 200석을 확보했다. 기민련 CDU 의 정당투표 숫자 12,447,656을 임시 나눔숫자 (divisor) 644로 나눴을 때 대략 181석이 된다.
기민련이 전국적인 정당투표 비율에 근거했을 때는 181석이지만, 실제로는 초과 의석 때문에 200석이 되었다. 이것을 보정해줄 필요가 있다. 기민련은 과대 대표되었고, 초과의석을 내지 못한 좌파당, 녹색당, 독일을 위한 대안 (AfD), 자민당(FDP)은 과소 대표되었기 때문이다.
기민련의 정당투표수 12,447,656을 200석으로 나누면, 62238이 된다. 이렇게 되면 기민련의 보정 의석은 0이 된다. 기민련에게는 추가 의석을 줄 필요가 없다.
이와는 대조적으로 다른 정당들은 보상 의석을 추가로 확보할 수 있게 된다.
독일 선관위는 62300 을 '선택된 나눔숫자 geeignete Divisor)'라고 했다. 각 정당 투표숫자를 6만 2300으로 나누면 획득해야 할 새로운 의석 숫자가 도출된다.사민당 19석, 녹색당 10석, 좌파당 10석, 자유민주당 15석, 독일을 위한 대안 (AfD) 등이 11석을 추가로 배정받았다.
결국 644석 중, 초과 의석 46석 때문에 발생한 불비례성을 바로잡기 위해서, 독일 선관위는 추가 의석수 65석을 투입하는 방법을 채택했다. 추가로 65석을 투입해서, 정당투표율과 의석숫자의 비율이 더 조응하도록 조치를 취한 것이다.
결국 644석에다 65석이라는 '보상-보정' 의석을 합쳐서 2017년 독일 연방 총선 최종 의석수 709석이 되었다.
소결: 한국에서는 당장 2017년 연방의회 선거에서, 독일처럼 ‘보상 의석’ 65석까지 투입하는 그런 방식을 쓸 필요는 없다.
오히려 한국에서 필요한 것은 지역구 대 정당명부 비례대표 비율을 독일처럼 1:1에서 출발할 수 있도록 선거법을 바꾸는 것이다.국회의원 정수 증가는 불가피하다.
당연히 현재 여론은 우호적이지 않을 수 있다. 하지만 국회가 자유한국당과 같은 무능한 특권집단이 아니라, 진정한 민의를 대변하는 입법자가 된다면 국회의원 정수는 인구 10만명 당 1명으로 늘려도 국민은 박수칠 것이다.
최종 당선자 숫자는 709석이다.
1표는 지역 후보자, 2번째 표는 정당투표이다.
아래는 권역별 의석 숫자를 제 1차적으로 결정하는 기준이 되는 정당투표율이다.
지역 후보자 당선 299명 중, 기민당 CDU 185, 사민당 SPD 59, 기사련 CSU 46, 좌파당 Linke 5, 녹색당 Grüne 1, 독일을 위한 대안(AfD) 3, 자유민주당 (FDP) 0 석을 획득했다.
지역 후보 투표 결과
709석의 과반 이상은 355석으로, 정부를 구성할 수 있는 의석 숫자이다. 2017년 총선 결과는 거대 양당 기민/기사 연합과 사민당이 하락해, 연립정부를 형성하는 수밖에 없게 되었고, 그 경우의 수가 6가지가 되었다.
2018년 현재 독일은
기민/기사 연합과 사민당이 대연정 (Große Koalition) 행정부를 만들었다.
Endgültige Sitzberechnung und Verteilung der Mandate bei der Bundestagswahl 2017
6.1 Sitzberechnung
6.1.
4 2. Oberverteilung: 초과 과잉 분배
Erhöhung der Gesamtzahl der Sitze für die Parteien
In der Oberverteilung der zweiten Stufe werden die Sitze auf Bundesebene auf die Parteien nach dem Anteil ihrer jeweiligen Zweitstimmen verteilt.
Die Verteilung erfolgt nach dem Verfahren Sainte-Lague/Schepers.
Hierbei gilt die Bedingung, dass jede Partei mindestens die in Tabelle 6.1.3 ermittelte garantierte Mindestsitzzahl auf Bundesebene erhält.
Hierfür ist ggf. eine Erhöhung der Gesamtsitzzahl notwendig.
Die Gesamtsitzzahl wird jedoch nur so weit erhöht, bis die Bedingung erfüllt ist.
Die einzelnen Schritte zur Ermittlung des endgültigen Divisors und der Divisorspanne finden Sie in Tabelle 6.2.3.
Zu berücksichtigende Zweitstimmen: 44.189.959
Mindestsitzzahl: 644
Anfangsdivisor: 44.189.959 : 644 = 68.617,949
Bei der Berechnung mit dem Anfangsdivisor würde die garantierte Mindestsitzzahl nicht für jede Partei erreicht werden.
Deshalb ist der Divisor herabzusetzen.
Mögliche Divisorspanne: > 62.202,275 und <= 62.394,266
Ausgewählter Divisor: 62.300
Partei Garantierte Mindestsitzzahl (Spalte 1) Zweitstimmen Divisor Sitze nach Erhöhung Erhöhung um ...
2017 독일 연방 의회 최종 의석 계산과 의원 분배
지역구 299석각 주 16개 권역별 정당 비례대표
정당들의 전체 의석 증가 :
- 생 라그 쉐퍼 방식에 따라서 분배한다.
총 정당투표 숫자는 44.189.959 (4천 418만 9959표)
644의석은 각 정당들이 지역구 당선자와 각 권역별 비례대표 당선자 숫자를 합친 숫자이다.
임시 나눔숫자 Divisor 는 44189959 나누기 644 = 68.617,949 이다. (약 6만 8618)
초기 임시 나눔숫자 계산에서, 보증 최소 의석이 각 정당에 돌아가지 않는다.
따라서 나눔숫자 (Divisor)는 68617 보다 적어진다.
나눔숫자 가능 마진은 62202.275와 62394.266 사이이다.채택된 나눔숫자는 62300 (6만 2300)이다.
1. Berechnungsschritt – Ermittlung der Obergrenze für die Divisorspanne:
Für jede Partei wird ein Divisor ermittelt, mit dem sie gerade so die Mindestsitzzahl erreicht.
Hierzu werden die Zweitstimmen der Partei durch die Mindestsitzzahl -0,5 dividiert. Man geht dabei davon aus, dass bei der Berechnung nach Sainte-Lague/Schepers eine ungerundete Sitzzahl von ,5 aufgerundet wird.
2. Berechnungsschritt – Ermittlung der Untergrenze für die Divisorspanne und des endgültigen Divisors: Die Untergrenze für die Divisorspanne bildet der Divisor, mit dem eine Partei einen Sitz mehr erhalten würde als mit dem Divisor aus dem 1. Berechnungsschritt. D. h. es muss zuerst eine Sainte-Lague/Schepers-Berechnung mit dem Divisor aus Schritt 1 durchgeführt werden um die endgültige Sitzzahl zu erhalten.
Anschließend werden die Zweitstimmen der Parteien durch die neu errechneten Sitzzahlen + 0,5 dividiert.
Der größte dieser Divisoren bildet die Untergrenze für die Divisorspanne.
Endgültige Sitzberechnung und Verteilung der Mandate bei der Bundestagswahl 2017
6.1 Sitzberechnung 6.1.4 2. Oberverteilung: Erhöhung der Gesamtzahl der Sitze für die Parteien In der Oberverteilung der zweiten Stufe werden die Sitze auf Bundesebene auf die Parteien nach dem Anteil ihrer jeweiligen Zweitstimmen verteilt. Die Verteilung erfolgt nach dem Verfahren Sainte-Lague/Schepers. Hierbei gilt die Bedingung, dass jede Partei mindestens die in Tabelle 6.1.3 ermittelte garantierte Mindestsitzzahl auf Bundesebene erhält. Hierfür ist ggf. eine Erhöhung der Gesamtsitzzahl notwendig.
Die Gesamtsitzzahl wird jedoch nur so weit erhöht, bis die Bedingung erfüllt ist. Die einzelnen Schritte zur Ermittlung des endgültigen Divisors und der Divisorspanne finden Sie in Tabelle 6.2.3. Zu berücksichtigende Zweitstimmen: 44.189.959 Mindestsitzzahl: 644 Anfangsdivisor: 44.189.959 : 644 = 68.617,949
Bei der Berechnung mit dem Anfangsdivisor würde die garantierte Mindestsitzzahl nicht für jede Partei erreicht werden. Deshalb ist der Divisor herabzusetzen. Mögliche Divisorspanne: > 62.202,275 und <= 62.394,266 Ausgewählter Divisor: 62.300
참고 자료: 독일 각 주별 배당 의석수, 기준은 각 주의 인구
참고 자료: 생라그 /쉐퍼즈 방식
https://www.bundeswahlleiter.de/en/service/glossar/s/sainte-lague-schepers.html
Sainte-Laguë/Schepers
The German physician Hans Schepers, at the time Head of the Data Processing Group of the German Bundestag, in 1980 suggested that the distribution of seats according to d’Hondt be modified to avoid putting smaller parties at a disadvantage. By a different calculation method, the procedure proposed by Schepers arrives at the same results as the method developed by the French mathematician André Sainte-Laguë in 1912.
The procedure according to Sainte-Laguë/Schepers has been used since 1980 for the distribution of seats in the committees and bodies of the German Bundestag. Since 2009, it is the procedure used to distribute the seats in Bundestag and European elections. It has been employed in the elections to the Länder parliaments of Bremen (since 2003), Hamburg (since 2008), Nordrhein-Westfalen (since 2010), Baden-Württemberg and Rheinland-Pfalz (since 2011) and Schleswig-Holstein (since 2012).
In this procedure, which is also called divisor method with standard rounding, the respective numbers of second votes cast for the individual parties are divided by a joint divisor.
The resulting quotients are rounded according to standard practice to obtain numbers of seats, i.e. the figure is rounded up or down when the remaining fraction is larger or smaller than 0.5, where the residual equals 0.5 exactly, a lot will be drawn. The divisor is determined in a way which ensures that the total of the numbers of seats equals the total of the seats to be distributed. Three different methods may be used for the calculation which produce the same result and thus are regarded as equal from the legal perspective:
- Highest average method: this method follows the train of thought on which the procedure according to d’Hondt is based, with the respective number of votes being divided by 0.5, 1.5, 2.5 etc. and the seats, in turn, being successively allocated by descending maximum numbers. The calculation according to d’Hondt is based on the full entitlement to a seat and therefore uses whole numbers for division, with smaller parties obtaining their first and further seats disproportionately late. In comparison, the requirements for a seat to be assigned have been lowered with this procedure. Once there is an entitlement to more than half a seat, it is already allocated.
- Rank order statistic procedure: here, the inverse values are considered instead of the maximum numbers and the seats are successively assigned according to these ascending rank order statistics.
- Iterative procedure: with this method, an approximate allocation is calculated in a first step. The total number of votes to be considered is divided by the total number of seats to be distributed, thus determining a provisional divisor for allocation. Any remaining discrepancies are reduced in the following steps by increasing or reducing the divisor until the final allocation has been found where the distribution of seats corresponds with the number of seats to be distributed.
For the distribution of seats in the elections to the German Bundestag, the legislator selected the last-mentioned iterative procedure when the procedure according to Sainte-Laguë/Schepers was introduced. For the above example, the distribution of seats would be calculated as follows:
Procedure in accordance to Section 6 (2) of the Federal Elections Act with divisor for allocation
Formula:
Determining the divisor for allocation (Criterion: allocation of as many seats to Land lists as there are seats to be distributed):
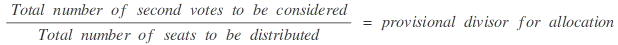 If necessary, increasing or reducing the divisor for allocation until the total calculated corresponds to the total of the seats to be distributed.Total number of seats minus the seats obtained by successful individual candidates (constituency nomination pursuant to Section 20 (3) of the Federal Elections Act) or successful party candidates, where the party has obtained less than five percent of the valid second votes and fewer than three direct seats or has not been admitted with a Land list in the respective Land (Section 6 (2) sentence 6 in conjunction with Section 6 (1) sentence 3 of the Federal Elections Act).
If necessary, increasing or reducing the divisor for allocation until the total calculated corresponds to the total of the seats to be distributed.Total number of seats minus the seats obtained by successful individual candidates (constituency nomination pursuant to Section 20 (3) of the Federal Elections Act) or successful party candidates, where the party has obtained less than five percent of the valid second votes and fewer than three direct seats or has not been admitted with a Land list in the respective Land (Section 6 (2) sentence 6 in conjunction with Section 6 (1) sentence 3 of the Federal Elections Act).
Example: Allocation of 8 seats
1st step:
| Party | Calculation | Result after standard rounding = seats to be distributed accordingly |
|---|---|---|
| A | 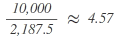 |
5 |
| B | 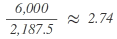 |
3 |
| C | 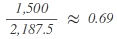 |
1 |
As a total of 9 seats is attributable to the parties when using the divisor 2,187.5 for allocation purposes while there are only 8 seats to be distributed, the divisor has to be increased until the calculation of the allocation of seats sums up to the number of seats to be distributed. To this end, the calculation is repeated with the higher divisor of 2,300:
2nd step:
| Party | Calculation | Results after standard rounding = seats to be distributed accordingly |
|---|---|---|
| A | 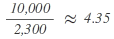 |
4 |
| B | 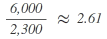 |
3 |
| C | 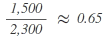 |
1 |
The procedure according to Sainte-Laguë/Schepers eliminates paradoxes that may occur when seats are distributed according to the Hare/Niemeyer method.
Last update: 1 August 2015
반응형